Probability Lab
Mit den Funktionen des Probability Lab können Sie praktische Wege entdecken, um Optionen zu verstehen und zu durchdenken – ganz ohne komplexe Rechenwege.
Auf dieser Seite möchten wir Ihnen die folgenden Konzepte vorstellen:
Wahrscheinlichkeitsverteilung (WV)
Sehen wir uns zuerst das Konzept der Wahrscheinlichkeitsverteilung (WV) an. Im Grunde sagt sie einfach nur aus, dass für alle zukünftigen Ergebnisse eine Möglichkeit, Chance bzw. Wahrscheinlichkeit besteht, dass sie tatsächlich eintreten. Die WV gibt genau an, wie hoch die Wahrscheinlichkeit ist, dass ein bestimmtes Ergebnis eintritt. Beispiele:
Wie hoch ist die Wahrscheinlichkeit, dass die Tageshöchsttemperatur in Hongkong am 22. November nächsten Jahres zwischen 21 und 22 Grad Celsius liegt?
Wir könnten dazu die Temperaturmessungen vom 22. November der letzten hundert Jahre zusammentragen. Ziehen Sie dazu eine horizontale Linie und markieren Sie darauf eine Skala von 16 bis 30 Grad. Zählen Sie dann, wie viele Temperaturmessungen in jedes Ein-Grad-Intervall fallen. Die Anzahl der Temperaturereignisse in jedem Intervall entspricht der prozentualen Wahrscheinlichkeit, dass die Temperatur am 22. November in diesem Intervall liegen wird. Dabei gilt die Annahme, dass der bisherige Verlauf auch in Zukunft gelten wird. Es funktioniert, weil wir mit 100 Messungen arbeiten. Andernfalls müsste das Ergebnis mit 100 multipliziert und durch die Gesamtzahl aller Messungen geteilt werden, um den Prozentwert zu erhalten. Für eine höhere Genauigkeit wären mehr Datenpunkte erforderlich. Wir könnten dann zum Beispiel Daten vom 20. bis 24. November verwenden.
Zeichnen Sie für jedes Grad-Segment eine horizontale Linie ein, sodass Balken entstehen. Die Höhe der Balken muss dabei jeweils der Anzahl der Datenpunkte im jeweiligen Segment entsprechen. Wenn wir die Daten vom 20. bis 24. November verwendet hätten, würden wir mehr Daten und eine bessere Genauigkeit erhalten. Allerdings müssten wir dann mal 100 und durch 500 rechnen.
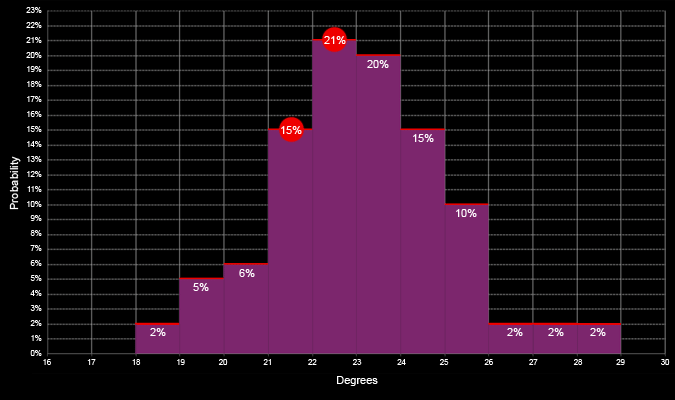
Die horizontalen Linien ergeben ein Balkendiagramm unserer WV. Sie geben an, wie hoch die Wahrscheinlichkeit (in Prozent) ist, dass sich die Temperatur in den jeweiligen Segmenten befinden wird. Wenn wir herausfinden möchten, wie hoch die Wahrscheinlichkeit ist, dass die Temperatur unterhalb eines bestimmten Niveaus liegen wird, müssen wir alle Wahrscheinlichkeiten der Segmente unterhalb dieser Grenze addieren. Analog addieren wir alle Werte oberhalb des gewählten Niveaus, um die Wahrscheinlichkeit dafür zu berechnen, dass die Temperatur über diesem Niveau liegen wird.
Folglich zeigt das Diagramm, dass die Wahrscheinlichkeit einer Temperatur zwischen 21 und 22 Grad Celsius bei 15 % und die Wahrscheinlichkeit einer Temperatur unter 22 Grad Celsius bei 2 + 5 + 6 + 15 = 28 % liegt. Die Wahrscheinlichkeit einer Temperatur über 22 Grad liegt bei 100 - 28 = 72 %.
Bitte beachten Sie, dass die Summe der Wahrscheinlichkeiten aller Segmente 1,00 ergeben muss. Das heißt, es besteht eine Wahrscheinlichkeit von 100 %, dass an diesem Datum irgendeine Temperatur in Hongkong vorherrscht.
Wenn wir mehr Daten hätten, könnten wir durch Verkleinern der Intervalle unsere WV weiter präzisieren. Dann würden die horizontalen Linien auf Punkte zusammenschrumpfen, die eine gleichmäßige glockenförmige Kurve bilden würden.
Aktienkurse
Ebenso wie man zukünftigen Temperaturspannen Wahrscheinlichkeiten zuweisen kann, ist dies auch bei den Kursspannen zukünftiger Aktien-, Rohstoff- und Währungskurse möglich. Es besteht jedoch ein wichtiger Unterschied. Während die Temperatur über Jahre hinweg generell einem berechenbaren Muster folgt, gilt dies nicht für Aktienkurse, da diese stärker durch grundlegende Faktoren und menschliche Einschätzungen beeinflusst werden.
Die Antwort auf die Frage „Wie hoch ist die Wahrscheinlichkeit, dass der Kurs von ABC am 22. November zwischen 21,00 und 22,00 liegen wird?“ ist verglichen mit der Temperaturvorhersage für Hongkong eher eine Schätzung.
Die uns zur Verfügung stehenden Informationen sind der aktuelle Aktienkurs, der bisherige Kursverlauf sowie Fundamentaldaten zu den Zukunftsaussichten des Unternehmens, der Branche, der Wirtschaft, der Währung und dem internationalen Handel sowie politische und weitere Aspekte, die die Meinung der Anleger/-innen über den Aktienkurs beeinflussen könnten.
Das Vorhersagen des zukünftigen Kurses einer Aktie ist eine ungenaue Angelegenheit. Bei der Vorhersage der WV zukünftiger Aktienkurse scheint es mehr Spielraum zu geben oder zumindest tritt der probabilistische Charakter dieses Vorhabens hier deutlicher hervor. Je mehr Informationen und Hintergrundwissen wir haben, desto besser sind die Chancen, richtig zu liegen.
Herleiten einer Wahrscheinlichkeitsverteilung bei Optionen
Die Preise von Put- und Call-Optionen auf Aktien werden durch eine WV bestimmt. Das Interessante daran ist aber, dass man diesen Prozess auch umkehren kann: Wenn man also die Preise von Optionen kennt, kann man daraus recht einfach eine implizite WV herleiten. Sie müssen nicht unbedingt wissen, wie das im Einzelnen funktioniert, und können daher den nächsten Abschnitt auch gern überspringen. Falls Sie es aber wissen möchten, finden Sie im Folgenden eine Methode, die auch schon für ältere Schüler/-innen nachvollziehbar sein sollte.
Nehmen wir an, dass die Aktie XYZ zu einem Kurs von 500 USD pro Aktie gehandelt wird. Wie hoch ist die Wahrscheinlichkeit (in Prozent), dass der Preis zum Verfallsdatum in etwa einem Monat zwischen 510 und 515 USD liegt? Angenommen, die Call-Option für den Kurs von 510 USD wird zu einem Preis von 6,45 USD gehandelt und die Prämie für die Option für 515 USD beträgt 4,40 USD. Sie können den Call für den Kurs von 510 USD kaufen und den für 515 USD verkaufen und zahlen dann 2,05 USD.
- Falls der Aktienkurs am Verfallsdatum unter 510 USD liegt, verlieren Sie 2,05 USD.
- Falls er zwischen 510 und 515 USD liegt, entspricht Ihr Gewinn dem Mittelwert Ihres Verlusts bei einem Kurs von 510 USD (d. h. -2,05 USD) und Ihrem Gewinn
bei einem Kurs von 515 USD (d. h. 2,95 USD), also 0,45 USD. - Falls er über 515 USD liegt, beläuft sich Ihr Gewinn auf 2,95 USD.
Nehmen wir darüber hinaus an, dass wir zuvor berechnet haben, dass die Aktie mit einer Wahrscheinlichkeit von 56 % bzw. 0,56* unter 510 USD liegen wird.
Sofern die Preise der Optionen „fair“ sind – d. h., wenn die WV des Markts korrekt ist, werden weder Gewinne noch Verluste gemacht –, dann ist 0,56 × -2,05 + X × 0,45 + Y × 2,95 = 0. Dabei ist X die Wahrscheinlichkeit, dass der Kurs zwischen 510 und 515 USD liegen wird, und Y die Wahrscheinlichkeit, dass er 515 USD übersteigen wird.
Da alle Kurse, die eintreten können, insgesamt eine Wahrscheinlichkeit von 100 % besitzen, ergibt sich aus 0,56 + X + Y = 1,00 eine Wahrscheinlichkeit von 0,06 für X und von 0,38 für Y.
* Um eine vollständige Wahrscheinlichkeitsverteilung zu berechnen, muss man mit dem niedrigsten Basispreis beginnen und eine Schätzung der Wahrscheinlichkeit für die darunterliegenden Preise vornehmen. Dabei sollte es sich um eine kleine Zahl handeln, damit Fehler nicht allzu hoch ausfallen können.
Wenn Sie bis hierher gelesen haben, möchten Sie jetzt sicher auch wissen, wie man den Preis jeder beliebigen Call- oder Put-Option aus der WV herleitet.
Für Call-Optionen können Sie den Aktienkurs in der Mitte jedes Segments über dem Basispreis nehmen, davon den Basispreis abziehen und das Ergebnis mit der Wahrscheinlichkeit multiplizieren, dass der Kurs in diesem Segment liegen wird. In Bezug auf das hintere Ende müssen Sie die geringe Wahrscheinlichkeit schätzen und einen Preis ansetzen, der etwa 20 % über dem hohen Basispreis liegt. Wenn Sie dann alle Ergebnisse addieren, erhalten Sie den Preis der Call-Option.
Für Put-Optionen können Sie den Aktienkurs in der Mitte jedes Segments unter dem Basispreis nehmen, diesen vom Basispreis abziehen und das Ergebnis wieder mit der Wahrscheinlichkeit multiplizieren. Für das letzte Segment zwischen Null und dem niedrigsten Basispreis würde ich 2/3 des niedrigsten Basispreises ansetzen und die Wahrscheinlichkeit schätzen. Dann werden wieder alle Ergebnisse addiert, um den Preis der Put-Option zu berechnen.
Manche werden einwenden, dass wir hier nur mit sehr groben Schätzungen arbeiten. Stimmt. So verhält es sich nun einmal mit Preisvorhersagen – sie sind von Natur aus ungenau. Und das sollte man auch nicht beschönigen. Wir schätzen alle nur. Niemand weiß es mit Sicherheit. Computerexperten mögen mit ihren komplexen Modellen Unwissende zu der Annahme verleiten, ihre Berechnungen wären präzise. Aber Tatsache ist, dass niemand die Wahrscheinlichkeiten genau kennt. Daher kann Ihre durchdachte Annäherung, die auf Ihrer eigenen Einschätzung der Lage beruht, letztendlich sogar besser sein, als die auf vergangenen Daten basierende Berechnung eines Modells.
Beachten Sie bitte, dass wir Zinseffekte in dieser Diskussion ignoriert haben. Wir haben darüber hinaus die Tatsache ausgeklammert, dass Optionen vorzeitig ausgeübt werden können, was sie wertvoller macht. Würde man die gesamte WV berechnen, müsste man diesen zusätzlichen Wert ebenfalls berücksichtigen. Allerdings ist er nur für Optionen relevant, die tief im Geld sind. Sie können das Problem aber einfach umgehen, indem Sie Calls zum Berechnen der WV für hohe Preise und Puts für niedrige Preise verwenden.
Die vom Markt implizierte WV und Ihre eigene Herleitung
Da die Put- und Call-Optionen der meisten Aktien an den Optionsmärkten gehandelt werden, lässt sich die WV für diese Aktien aus den vorherrschenden Optionspreisen ableiten. Ich nenne das die „WV des Markts“, weil sie sich durch den Konsens der Optionskäufer und -verkäufer ergibt, selbst wenn viele sich dessen nicht bewusst sind.
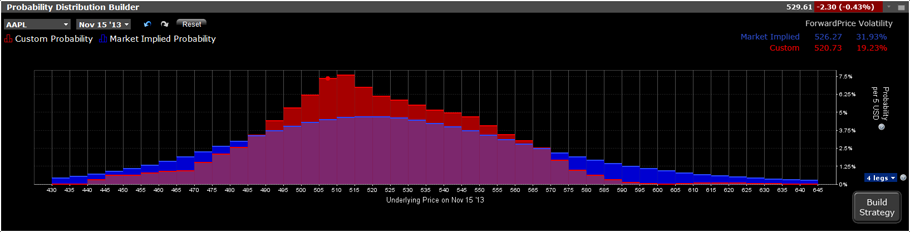
Der höchste Punkt auf der vom Markt implizierten WV-Kurve liegt tendenziell nahe am aktuellen Aktienkurs (zzgl. Zinsen abzgl. Dividenden). Je weiter Sie sich von diesem Punkt nach rechts oder links bewegen, desto stärker verringern sich die Wahrscheinlichkeiten – zunächst nur langsam, dann schneller und schließlich wieder langsamer, wobei der Wert 0 jedoch nie ganz erreicht wird. Der Forward-Kurs ist der zum Verfall erwartete Kurs, so wie er von der WV impliziert wird.
Klicken Sie auf die Abbildung, um die Ansicht zu vergrößern
Die Kurve ist nahezu symmetrisch, abgesehen davon, dass leicht höhere Kurse eine höhere Wahrscheinlichkeit aufweisen als leicht niedrigere Kurse und deutlich höhere Kurse eine geringere Wahrscheinlichkeit haben als Kurse, die nahe 0 liegen. Der Grund dafür ist, dass Kurse tendenziell schneller fallen als steigen und dass bei allen Unternehmen immer eine gewisse Wahrscheinlichkeit eines Totalausfalls besteht.
Im Probability Lab können Sie die WV anzeigen, die wir basierend auf den am Markt vorherrschenden Optionspreisen für alle Aktien oder Rohstoffe berechnen, für die Optionen angeboten werden. Geben Sie dazu einfach das entsprechende Symbol ein.
Die WV-Kurve ändert sich in dem Maße, wie sich Angebot und Nachfrage der Optionen an den Börsen verändern. Nun können Sie den horizontalen Balken in jedem Intervall nach oben oder unten verschieben, wenn Sie der Meinung sind, dass die Wahrscheinlichkeit, dass der Kurs in diesem Intervall liegen wird, geringer oder höher ist als die Konsensschätzung des Markts. Sie werden feststellen, dass sich alle anderen Balken mitbewegen, sobald Sie einen der Balken verschieben, wobei sich weiter entfernte Balken in die entgegengesetzte Richtung bewegen, da die Summe aller Wahrscheinlichkeiten 1,00 ergeben muss. Bitte beachten Sie ebenfalls, dass die WV des Markts weiterhin blau dargestellt wird, wohingegen Ihre Prognose rot erscheint. Sie können die Ansicht auch zurücksetzen, um all Ihre Änderungen rückgängig zu machen.
Der Markt tendiert zur Annahme, dass alle WV nahe dem statistischen Durchschnitt vergangener Ergebnisse liegen, sofern nicht sicher eine Kapitalmaßnahme bevorsteht, wie z. B. eine Fusion oder Übernahme. Wenn Sie den Markt oder die Daten bestimmter Aktien, Branchen oder Rohstoffe verfolgen, werden Sie ggf. zu einem anderen Schluss kommen. Es ist nicht auszuschließen, dass Sie gelegentlich zu anderen Einschätzungen kommen, was die Wahrscheinlichkeit bestimmter Ereignisse und die daraus folgenden Kursentwicklungen betrifft. Dieses Tool gibt Ihnen die Möglichkeit, Ihre Einschätzung zu grafisch darzustellen und auf dieser Basis zu handeln. Falls Ihre Einschätzung der WV nicht von derjenigen des Markts abweicht, sollten Sie nicht handeln, da bei jedem Trade, der auf Basis der Markt-WV getätigt wird, ein Gewinn von Null (abzgl. Transaktionskosten) zu erwarten ist. Die Summe aller möglichen Ergebnisse (Gewinn oder Verlust in jedem Intervall) multipliziert mit der dazugehörigen Wahrscheinlichkeit entspricht dem statistisch zu erwartendem Gewinn. Bei Verwendung der Markt-WV ist dieser Wert für jeden Trade gleich Null. Sie können einen beliebigen, tatsächlich ausgeführten Trade als Beispiel nehmen und sich den zu erwartenden Gewinn selbst ausrechnen, um sich von der Richtigkeit dieser Aussage zu überzeugen. Jedes Mal, wenn Sie bei einem Trade einen Gewinn erwarten, gehen Sie also im Grunde eine Wette ein, dass die WV des Markts falsch und Ihre Einschätzung korrekt ist. Dies trifft zu, egal, ob Sie sich dessen bewusst sind oder nicht. Von daher lohnt es sich durchaus, sich diese Tatsache ins Bewusstsein zu rufen und die eigenen Fähigkeiten mithilfe dieses Tools zu trainieren.
Die besten Trades und ihre möglichen Folgen
Sie können gern selbst ausprobieren, die Balken im Diagramm zu verschieben. Wir zeigen Ihnen Trades mit Kombinationen an, die gemäß Ihrer WV vielversprechende Ergebnisse erwarten lassen. Sie können angeben, ob wir Ihnen die „optimalen Trades“ anzeigen sollen, die aus Kombinationen von bis zu zwei, drei oder vier Optionslegs bestehen. Wir zeigen Ihnen die drei besten kombinierten Trades an sowie den jeweils erwarteten Gewinn, das Sharpe-Maß, die Nettobelastung oder Nettogutschrift, die prozentuale Wahrscheinlichkeit eines Gewinns, den maximalen Gewinn und maximalen Verlust und die mit jedem Trade verbundenen Wahrscheinlichkeiten auf Basis Ihrer WV und die entsprechende Margin-Anforderung.
Die besten Trades sind die mit dem höchsten Sharpe-Maß oder dem höchstmöglichen Verhältnis zwischen erwartetem Gewinn und Variabilität des Ergebnisses. Bitte denken Sie daran, dass der erwartete Gewinn definiert wird als die Summe des Gewinns oder Verlusts multipliziert mit der entsprechenden Wahrscheinlichkeit, die Sie für alle Kurse festgelegt haben. Die untere Kurve zeigt den vorhergesagten Gewinn oder Verlust, der sich aus diesem Trade ergeben würde, sowie die entsprechende Wahrscheinlichkeit für jeden Preispunkt.
Die interaktive Kurve unten ist eine grobe Simulation unserer echtzeitbasierten Probability-Lab-Anwendung, die wir unserer Kundschaft bereitstellen. Ebenso werden die „besten Trades“ ausschließlich zu Veranschaulichungszwecken angezeigt. Anders als in der eigentlichen Anwendung sind diese nicht für Ihre Verteilung optimiert.
Wenn Ihnen ein Trade in unserer App zusagt, können Sie einfach die Menge erhöhen und die Order übermitteln.
Kostenloses Probability Lab für alle ohne Kundenkonto
In den nächsten Versionen dieses Tools werden wir Buy-Writes, Delta-Umschichtungen, Kombinationen mit mehreren Verfallsterminen, Verlängerungen fällig werdender Positionen und weitere Verbesserungen in Angriff nehmen.
Wir empfehlen, das interaktive Tool selbst zu testen. Beim Ausprobieren werden Sie Ihr Verständnis der Optionspreisbildung vertiefen und Ihr „Gefühl für den Optionsmarkt“ schärfen.
Die vom Probability Lab erstellten Prognosen und anderen Informationen zur Wahrscheinlichkeit bestimmter Anlageergebnisse sind rein hypothetischer Natur. Sie bilden weder tatsächliche Anlageergebnisse ab noch garantieren sie eine bestimmte Performance in der Zukunft. Bitte beachten Sie, dass die mit diesem Tool erzielten Ergebnisse im Laufe der Zeit unterschiedlich ausfallen können.